第4回春の方法論セミナー「効果の科学からデータ生成過程の科学へ
~心理学者のためのベイジアン・モデリング入門」
日時
2017年3月14日(火) 13時~17時半(12時半開場予定)
会場
上智大学四ツ谷キャンパス3号館5階521室 ※アクセスマップ
参加費
無料(事前予約不要;会員以外の参加も可)
企画
日本社会心理学会新規事業委員会
講師
岡田謙介(専修大学人間科学部 心理統計学)
国里愛彦(専修大学人間科学部 計算論的臨床心理学)
企画メッセージ
構成と講演要旨(動画・資料)はこちら
今、ベイズが熱い
ここ1〜2年の間、ベイジアン・モデリングに関する和書が相次いで出版された。大御所による教科書(豊田 2015, 2017)から気鋭のデータサイエンティストによる実践的なテキスト(松浦 2016)まで、どれも分かりやすいと評判が良い。ネット上でも、Stan, MCMCを使った実践的な分析を紹介するスライドが数多く公開され、学習環境が急激に整ってきた。今、ベイズが熱い。
だが、自習できる環境が整備されたとは言っても、そもそもベイズを学ぶ必要があるのか?自分にとって役立つのか?良く分からない人も多いはずである。本セミナーの目的は、ベイジアン・モデリングの意義とその位置づけを、理解していただくことにある。
結論から述べておこう。心理学者にとってのベイジアン・モデリングとは、心理学者を縛り続けてきた「実験操作や介入の効果を検証する」という科学観から我々を解き放つ、新しい方法論上のパラダイムである。大言壮語だと切り捨てる前に、本解説を読んで頂きたい。
ベイズに対する大きな誤解
「SPSSのようにお手軽にベイズ統計を行う」という目的の下、JASPというフリーの統計ソフトの開発が進められている。このソフトをインストールしてみると、次のようなメニューが目に入る。
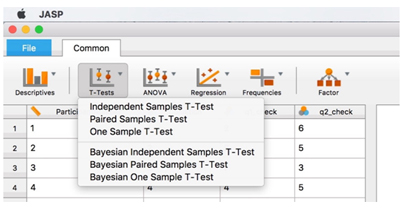
t検定や分散分析というメニューの下に、従来の推測統計に基づくt検定とベイジアンt検定が対比されている。
これを見て次のように感じる人もいるだろう。「そうか。ベイズ統計とはp値の代わりにベイズ・ファクターを求めて、効果の有無を見る分析なのだ」、と。たとえば、Bemの超能力実験のデータは、ベイズ・ファクターを用いて再分析された。そして、「超能力が存在する」という彼の主張を支持するほど、強い実験データではないことが指摘されている(Rouder & Morrey, 2011)。これは頻度論に基づく従来の統計では得られなかった結論である。
こうした使い方を見ていれば、「ベイズ統計は、従来の統計よりも適切に効果の有無を検証できる。だから流行っているのだ」と思う人も出てくるだろう。だが、これは大きな間違いである。
統計モデルとベイズ統計モデル
まず、用語を定義しよう。たとえば一般線形モデルを想像していただきたい。従属変数と独立変数を指定してモデルを作る。そして主効果や交互作用などの効果(パラメータ)を推定する。多くの場合、パラメータは最尤推定によって求められる。これが我々のよく知る統計モデルである。ここで最尤推定の代わりに、ベイズ推定を用いるのが、ベイズ統計モデルである。
「ちょっと待て」と言いたい人も出てくるだろう。「モデルが同じなら、効果の推定方法なんて些細な違いではないのか?ユーザーとして知りたいのは、モデルにおける効果の有無だ。効果(パラメータ)推定の方法なんて、どうでも良い。そんなことで騒いでいるとは…やれやれ、統計オタクはこれだから…」
だが、そうは問屋は卸さない。第2回春の方法論セミナーで一般化線形混合モデルを学んだ方はピンと来るかも知れないが、統計モデルが複雑になると、最尤推定ではパラメータ推定が困難になってくる。だが、ベイズ推定を使えば、統計モデルが複雑になっても、パラメータ推定が可能となるのである。些細な技術論に聞こえるかもしれない。だが、より複雑なモデルを容易に利用できることが、科学という営みにもたらす影響は甚大である。
ベイジアン・モデリングとは
ここまで来れば、理解していただけるだろう。ベイジアン・モデリングとは、データを記述するためのモデルを作り、そのパラメータをベイズ推定する研究アプローチ全般を指す。認知科学で用いられているような認知モデルを作り、そのパラメータをベイズ推定すれば、それはベイジアン認知モデルと呼ばれる。生物種の系統を再現することに関心がある生物学者は、系統樹のモデルを作りパラメータをベイズ推定する。ベイズ系統推定と呼ばれる手法である。
モデルが複雑になっても、階層構造が導入されても、潜在変数がモデルの中に組み込まれても、ベイジアン・モデリングによって、これまでにないほど複雑で多様なモデルを用いた分析が可能となる。特に、WinBugs, JAGS, Stanといったソフトウェアの登場により、MCMC(マルコフ連鎖モンテカルロ)に基づいて容易にベイズ推定ができるようになったことで、この流れは決定的なものとなった。
効果の科学からデータ生成過程の科学へ
心理学者が慣れ親しむ統計モデルの多くは、変数の足し算(主効果)と掛け算(交互作用)だけで現象を表現する。科学者が世界を理解するために用いる理論は、その時代に利用できる研究手法に大きく制約される (Gigerenzer, 1991)。頻度論に基づく統計ばかりが利用される時代が長く続いていたため、我々は変数の足し算と掛け算(主効果と交互作用)だけで世界を理解するように訓練されてきた。そして実験的操作や介入など、効果の有無を検証することこそ、科学だと考えるように育成されてきたのである。
ベイズ推定が簡単に利用できることによって、「効果の有無で世界を見る」という科学観に囚われる理由は消失する。現象を表現するモデルそのものを作り、評価できるようになった。他にもメリットがある。最尤推定ではデータ数が少ないと推定できないケースでも、ベイズならばどうにか推定してそれなりの結論を導き出せる。これがどれだけ大きなメリットをもたらすか、日々データを触っている人ならば、すぐに理解できることだろう。
もちろん、まだまだ技術的な制約は存在している。だが効果の有無を検証する科学ではなく、データが生成される過程を明らかにする科学へ向かうための入り口が、近年の技術革新によって、多くの科学者に対して広く開かれるようになったのである。
本セミナーで伝えたいメッセージ
これまでベイズ統計が紹介される際、頻度論とベイズ主義の違い、あるいはベイズ主義の理解しやすさなどが語られることが多かっただろう。だがここまで説明したように、今ベイズが熱い理由は、全く別のところにある。第4回春の方法論セミナーの目的は、この大きなメッセージを、具体例を通して理解していただくことにある。
効果の有無では捉えきれない重要な問いが、科学には存在している。今の心理学は、それを問うようには作られていないだけである。そのため、「実験操作や介入といった効果の有無」だけで科学の世界を完結させようとする限り、ベイジアン・モデリングの恩恵を被ることは少ないかも知れない。だが「効果の有無」では捉えきれない問いに関心を持ち始めたら、もうベイジアン・モデリングなしでは生きていけなくなるかもしれない。
(竹澤正哲・清水裕士)
司会
竹澤正哲・清水裕士
構成と講演要旨
導入(竹澤・清水)
以下2つの講演の導入となる情報を提供する。まずベイジアン・モデリングに慣れてもらうために、ベイズ推定の利点,ベイズ推定を可能にする確率的プログラミング言語であるStanを紹介する。そしてStanを用いて、我々が良く知る様々な統計的検定がベイジアン・モデリングの枠組みの中でどのように行えるのか例示する。それらを通して,ベイジアン・モデリングという枠組みからデータを分析すると、従来困難であったような複雑な統計モデルでも、容易に分析できることをデモンストレートしていく。
調査データのベイジアン・モデリング(岡田謙介)
動画(前半のみ)・資料
このセミナーでは,私たちの行っている,調査データを対象としたベイジアン・モデリングの研究を,大きく分けて2つご紹介します。
ひとつめは,参加者が回答する項目数のモデリングです。この研究は少し変わっています。というのも,心理学研究としては比較的大規模な調査データ(数万人,数百項目)を分析するのですが,私たちの関心は,参加者がどう調査項目に回答したかではなく,どの時点で調査項目に回答するのをやめたかにあるからです。Webを使ったデータの取得が容易になり,また再現性の観点などからいわゆるMany Labs型の研究も増えている現在,回答する項目数の個人差に注目すると,もしかすると新しい心理学研究が開けてくるかもしれません。当初はデータをよく説明できていなかったモデルが,新たなアイディアを取り入れて改善されていく過程を追体験していただけたらと思います。
もうひとつは,尺度使用における個人差のモデリングです。心理学研究では,リッカート法の評定尺度を用いた調査が数多く行われています。しかし,リッカート尺度の各段階が,参加者の間で同じ心理量に対応しているのか,という根本的な疑問も実はあります。私たちはこの問題に対して,自分についての尺度評定に加え,第三者についての尺度評定も行ってもらうデータ(係留ビネットデータ)を得て,項目反応理論の考え方を応用したベイジアン・モデリングを行いました。この方法によって,尺度使用についての個人差と,共通尺度上での心理量とを分けて推定することが可能になります。モデル比較によって見えてくる知見も含めて,実際の研究例をお話できればと思います。
ベイジアン・モデリングと計算論的臨床心理学(国里愛彦)
動画・資料
このセミナーでは,計算論的臨床心理学とそこで用いられるベイジアン・モデリングについてご紹介します。
まず,計算論的臨床心理学という学問分野をご存知でしょうか?おそらく初めて聞いたという方が多いのではないでしょうか?精神医学においては,2000年代後半から,計算論的アプローチを精神医学に適用する計算論的精神医学という分野が提唱され,広がりを見せてきています。心は単純に脳などの生物学的基盤に対応づけることが難しく,また生物学的な基盤における各水準間にもギャップが存在します。これらの心理と生物学的基盤や生物学的基盤間のギャップを埋める際に,数理モデルなどを用いた計算論的アプローチは有用なツールになります。計算論的精神医学に比べて,計算論的臨床心理学という名前はあまり広まっているとは言い難い状況です。しかし,精神医学と臨床心理学には共通する問題も多いことから,計算論的精神医学と同様な理由で,計算論的臨床心理学があっても良いのではないかと思われます。このセミナーにおいては,計算論的臨床心理学において採用する計算論的アプローチの概要についてご紹介します。
次に,計算論的アプローチを用いた臨床心理学研究についてご紹介したいと思います。特に,計算論的アプローチの中でも,機械学習の1つである強化学習を用いた計算論的臨床心理学研究についてお話をします。具体的には,(1)意思決定過程への抑うつや不安などの影響に関して,強化学習モデルを用いて,一連の行動の背後にあるパラメータを推定するモデルベーストアプローチ,(2)行動の背後にあるパラメータ推定においてベイジアン・モデリングを使う利点と方法,(3)強化学習モデルと反応時間に関する数理モデルを統合した少し発展的な解析手法についてご紹介をしたく思います。
